- Se puede cambiar la forma del trángulo inicial moviendo sus vértices.
- Siempre se cumple el teorema: mismas áreas.
- Al mover los deslizadores se pueden girar los triángulos hasta 90 grados.
- Se pueden mostrar u ocultar los cuadrados.
- Se puede ver la construcción 'paso a paso'. .
lunes, 18 de agosto de 2025
Teorema de Snover (2000)
sábado, 21 de junio de 2025
Selectividad Ciencias Sociales Curso-2024-2025
lunes, 16 de junio de 2025
Selectividad Ciencias-Curso 2024-2025
viernes, 23 de mayo de 2025
La parábola y el producto de dos números
- Se pueden mover los puntos A y B para obtener el punto C.
- Se puede ver la construcción 'paso a paso'. .
miércoles, 19 de marzo de 2025
Triangulación de polígonos
domingo, 29 de septiembre de 2024
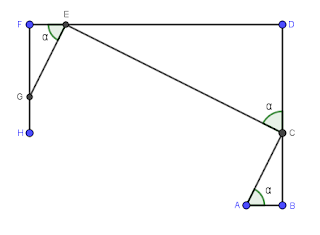
Problema de Thanos Kalogerakis (2017)
En primer lugar, ADME es un cuadrado porque, debido a que M es el punto medio del arco que subtiende el ángulo BAC (que es recto), los ángulos DAM=EAM=45º y, posteriormente, dado que ADME es claramente un rectángulo, los ángulos AMD=AME=45º, lo que hace que ADME sea un cuadrado. $$AB=AD-BD=MD-BD$$ $$AC=AE+EC=MD+EC$$ $$AB+AC=2MD+EC-BD$$ Los triángulos BMD y CME son iguales al ser rectángulos, MD=ME y los ángulos CME=BMD. Por tanto EC=BD. $$AB+AC=2MD \rightarrow \frac{AB}{MD}+\frac{AC}{MD}=\frac{AB}{MD}+\frac{AC}{ME}=2$$
- Se pueden mover el centro del círculo y el punto C para dimensionar y desplazar la figura.
- Moviendo el punto A a lo largo del semicírculo se comprueba la propiedad.
- Se puede ver la construcción 'paso a paso'. .
sábado, 15 de junio de 2024
Selectividad Ciencias-Curso 2023-2024
viernes, 22 de marzo de 2024
Puntos y segmentos
 |
| Soluciones |
martes, 30 de enero de 2024
Teorema de Conway
- Se prolonga el segmento AB hasta F, siendo AF=AP (azul)+PF (rojo).
- Se prolonga el segmento AB hasta I, siendo BG=BL (verde)+LI (azul).
- Se prolonga el segmento BC hasta H, siendo BH=BK (verde)+KH (azul).
- Se prolonga el segmento BC hasta D, siendo CD=CN (rojo)+ND (verde).
- Se prolonga el segmento CA hasta G, siendo AG=AJ (azul)+JG (rojo).
- Se prolonga el segmento CA hasta E, siendo CE=CM (rojo)+ME (verde).
- SF=AS (verde)+AP (azul)+PS (rojo)
- SI=SB (rojo)+BL (verde)+LI (azul)
- QD=QC (azul)+CN (rojo)+ND (verde)
- QH=QB(rojo)+BK (verde)+KH (azul)
- RE=RC (azul)+CM (rojo)+ME (verde)
- RG=RA (verde)+AJ (azul)+JG (rojo)
- Se pueden mover los vértices del triángulo.
- Se puede ver la construcción 'paso a paso'.
- Se pueden mover los vértices del triángulo.
- Se puede desplazar el punto hueco y al situarlo sobre el incentro se obtiene una circunferencia.
miércoles, 11 de octubre de 2023
Teorema de Mickey Mouse
domingo, 25 de junio de 2023
Selectividad Ciencias-Curso 2022-2023
viernes, 6 de enero de 2023
Disección de Dudeney (II)
- Se construye el triángulo equilátero ABC
- Se obtienen los puntos medios D y E de los lados AB y BC.
- Se trazan las rectas perpendiculares al lado AC que pasan por D y E.
- Se obtienen los puntos de intersección F y G sobre el lado AC.
- Se traza el segmento EF.
- Se trazan las perpendiculares desde D y G sobre el segmento EF.
- Se obtienen los puntos de interesección H e I.
- Moviendo los deslizadores se puede convertir el triángulo en un cuadrado.
- Dada la medida del lado del triángulo (AB) y del segmento (GI) se puede comprobar que estos valores están de acuerdo con que el segmento es la mitad del lado del cuadrado.
- Se prolonga la altura AE hasta J, de forma que EJ=EB=1 y K es el punto medio de AJ
- Se traza el círculo de centro K y radio AK: $$AK=\frac{1}{2}(AE+EJ)=\frac{\sqrt{3}+1}{2}$$
- Se prolonga BE hasta M y se obtiene el triángulo EMK donde: $$MK=\frac{\sqrt{3}+1}{2}$$ $$EK=AE-AK=\sqrt{3}-\frac{\sqrt{3}+1}{2}=\frac{\sqrt{3}-1}{2} $$
- Aplicando el teorema de Pitágoras: $$EM=\sqrt{\frac{\sqrt{3}+1}{2})^2-(\frac{\sqrt{3}-1}{2})^2}=\sqrt[4]{3} $$
- Se traza el círculo de centro E y radio EF=EM. Y si 'alfa' es el ángulo EFC, aplicando el teorema del seno: $$sen(\alpha)=\frac{sen(60)·EC}{EF}=\frac{\sqrt{3}/2·1}{\sqrt[4]{3}}=\frac{\sqrt[4]{3}}{2}$$
- FG=EC=1 y GI es perpendicular a FE: $$GI=FG·sen(\alpha)=1·\frac{\sqrt[4]{3}}{2}=\frac{\sqrt[4]{3}}{2}$$
lunes, 10 de octubre de 2022
Teorema de Von Schoonen
- Los puntos A y B permiten cambiar la posición y el tamaño de la figura.
- El punto D se puede desplazar por la circunferencia.
- Se puede ver la construcción 'paso a paso'.
miércoles, 15 de junio de 2022
Selectividad Ciencias-Curso 2021-2022
viernes, 27 de mayo de 2022
En el espíritu de Wasan (II)
Veamos otro ejemplo sencillo que también utiliza el teorema de Pitágoras.
Una circunferencia es tangente interior a una circunferencia mayor y a su diámetro. Construir la circunferencia tangente a ambas y a ese diámetro y expresar su radio en función de la circunferencia mayor.
Sea R el radio de la circunferencia mediana de centro E y r el radio del la circunferencia buscada. En el triángulo ADE, aplicando el teorema de Pitágoras, se tiene:
$$(R+r)^2=AD^2+(R-r)^2 \rightarrow 4Rr=AD^2$$
De forma análoga, en el triángulo ABC se tiene:
$$(2R-r)^2=BC^2+r^2 \rightarrow 4R^2-4Rr=BC^2$$
Como AD=BC se tiene que:
$$4R^2-4Rr=4Rr \rightarrow 4R^2=8Rr \rightarrow R=2r$$
Entonces el centro A, del la circunferencia buscada, se puede obtener como intersección de dos circunferencias de centros C y E y de radio 3R/2.
- Los puntos azules permiten cambiar la posición y el tamaño de la figura.
- Se puede ver la construcción 'paso a paso'.
lunes, 18 de abril de 2022
En el espíritu de Wasan (I)
Hay una palabra, wasan, que utilizan los japoneses para referirse a sus matemáticas frente a yosan o matemáticas occidentales. Aunque el wasan se debe a varios matemáticos japoneses, los iniciadores son Kambei Mori (principio siglo 17) y Yoshida Mitsuyoshi (1598-1672). Veamos un ejemplo sencillo que utiliza el teorema de Pitágoras.
Los centros A y B de dos círcunferencias iguales están en la circunferencia de la otra. Construir una circunferencia tangente a la recta AB, a la circunferencia de centro A interiormente y a la circunferencia de centro B exteriormente.
Llamamos AB=a, AF=x y GF=r (el radio de la circunferencia buscada). En el triángulo BFG, aplicando el teorema de Pitágoras, se tiene:
$$(a+r)^2=r^2+(a+x)^2$$
y , de forma análoga, en el triángulo AFG se cumple:
$$ (a-r)^2=r^2+x^2$$
Simplificando ambas ecuaciones y restando se obtiene:
$$4ar=a^2+2ax \rightarrow x+ a/2=2r$$
Significa que el lado EF del cuadrado ACDE, siendo C el punto medio del segmento AB, es un diámetro de la circunferencia buscada. Por tanto es fácil su construcción.
- Los puntos A y B permiten cambiar la posición y el tamaño de la figura.
- Se puede ver la construcción 'paso a paso'.
lunes, 28 de febrero de 2022
Método de Lill
El ingeniero y oficial del ejército austríaco Eduard Lill (1830-1900) ideó en matemáticas un procedimiento gráfico para determinar las raíces reales de un polinomio, que en esencia es una representación gráfica del algoritmo de Horner. Publicó su invento en 1867 en la revista francesa 'Nouvelles Annales de Mathématiques', y Charles Hermite proporcionó una descripción del mismo para el 'Compes rendus' del mismo año. Más tarde se conoció como el método de Lill.
El método de Lill implica expresar los coeficientes de un polinomio como magnitudes de una secuencia de segmentos en ángulos rectos entre sí. Encontrar las raíces se convierte en la realización de un problema geométrico. Vamos a explicarlo con el siguiente polinomio:
$$p(x)=1x^3+5x^2+7x+3$$
Siempre se puede hacer que el coeficiente de la potencia más alta sea la unidad, basta dividir todo el polinomio por ese valor. Se construye un primer segmento AB=1 y a continuación se construyen los segmentos perpendiculares correspondientes a los demás coeficientes del polinomio de la siguiente forma:
Hacia arriba BD=5, hacia la izquierda DF=7 y hacia abajo FH=3 porque todos los coeficientes son positivos. Cuando son negativos, se construyen en el sentido contrario a partir del extremo B. Se traza un segmento AC con el extremo en un punto cualquiera del segmento BD. Se traza el segmento CE perpendicular a AC y el segmento EG perpendicular a CE.
$$tg (\alpha)=\frac{BC}{AC}=\frac{BC}{1}=BC=-x$$
$$tg (\alpha)=\frac{BC}{AC}=\frac{BC}{1}=BC=-x \rightarrow CD=5-(-x)=5+x$$
$$tg (\alpha)=\frac{DE}{CD}=\frac{DE}{5+x}=-x \rightarrow DE=-x(5+x) \rightarrow EF=7+x(5+x)$$
$$tg (\alpha)=\frac{FG}{EF}=\frac{FG}{7+x(5+x)}=-x \rightarrow FG=-x(7+x(5+x)) \rightarrow $$
$$GH=3+x(7+x(5+x))=3+x(7+5x+x^2)=3+7x+5x^2+x^3$$
Es decir, obtenemos el polinomio pero expresado según el algoritmo de Horner.Si se divide el polinomio por x+2, se tiene:
$$\frac{1x^3+5x^2+7x+3}{x+2}=1x^2+3x+1+\frac{1}{x+2}$$
- Moviendo el punto azul se obtienen dos raíces diferentes.
- Se puede ver o no la obtención de la otra raíz doble.
- Moviendo el punto rojo se obtiene la segunda raíz doble.
- Se puede ver la construcción 'paso a paso'.
- Se puede ver la construcción 'paso a paso'.
viernes, 21 de enero de 2022
Períodos de Pisano
La operación módulo da el resto de una división entera: $$14 \mod 3 =2$$ donde 2 es el resto de dividir 14 entre 3.
Para la sucesión de Fibonacci: $$0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181...$$ la sucesión de restos, es siempre periódica: $$F_i \mod n$$
- restos modulo 2: $$0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1...$$
- restos modulo 3: $$0,1,1,2,0,2,2,1,0,1,1,2,0,2,2,1,0,1,1,2,0,2,2,1...$$
- restos modulo 4: $$0,1,1,2,3,1,0,1,1,3,2,1,0,1,1,3,2,1,0,1,1,2,3,1...$$
- restos modulo 5: $$0,1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0,1,1,2...$$
- restos modulo 6: $$0,1,1,2,3,5,2,1,3,4,1,5,0,5,5,4,3,1,4,5,3,2,5,1...$$
- restos modulo 7: $$0,1,1,2,3,5,1,6,1,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1...$$
- restos modulo 8: $$0,1,1,2,3,5,0,5,5,2,7,1,0,1,1,2,3,5,0,5,5,2,7,1...$$
- restos modulo 9: $$0,1,1,2,3,5,8,4,3,7,1,8,0,8,8,7,6,4,1,5,6,2,8,1...$$
En el caso de módulo 10, el periodo es: $$\pi(10)=\pi(2)\cdot\pi(5)=3\cdot 20=60$$ y el ciclo tiene 4 ceros y por tanto la figura es es simétrica.
- Se puede ver la construcción 'paso a paso'.
jueves, 25 de noviembre de 2021
La disección de Dudeney
Enseñó [el mercero] un trozo de tela con forma de triángulo equilátero perfecto, como se ve en la ilustración y dijo: “¿Es alguno de vosotros diestro en el corte de género? Estimo que no. Cada hombre a su oficio, y el estudioso puede aprender del lacayo, y el sabio del necio. Mostradme, pues, si podéis, de qué manera puede cortarse este trozo de género en cuatro piezas, para que puedan reunirse y formar un cuadrado perfecto”.
Proceso de disección propuesto por Dudeney a partir del triángulo equilátero ABC:- Marcar los puntos medios D y E de los AB y BC, respectivamente.
- Prolongar el segmento AE hasta el puto F tal que EF=EB.
- Marcar el punto medio G del segmento AF y trazar el arco de circunferencia de centro G y radio GF=AG.
- Prolongar el segmento CB hasta que corte el arco de circunferencia en H.
- Trazar el arco de circunferencia con centro E y radio EH hasta que corte el lado AC en J.
- Determinar el punto K tal que JK=AD (=DB=BE=EC).
- Trazar el segmento JE.
- Trazar desde D y K los segmentos perpediculaes al segmento JE, dando lugar a los puntos L y M (los segmentos serían DL y KM).
- Los polígonos de la disección son: 1. DBEL, 2. ADLJ, 3. JMK y 4. KMEC.
- Se puede ver la obtención de la disección 'paso a paso'.
- Moviendo las barras de desplazamiento se obtiene el cuadrado.