jueves, 17 de noviembre de 2022
Sucesiones de 'Somos'
lunes, 10 de octubre de 2022
Teorema de Von Schoonen
- Los puntos A y B permiten cambiar la posición y el tamaño de la figura.
- El punto D se puede desplazar por la circunferencia.
- Se puede ver la construcción 'paso a paso'.
lunes, 29 de agosto de 2022
Modelos de urnas
- Si c>0 el éxito y el fracaso son contagiosos, en el sentido de que un éxito o un fracaso aumenta la probabilidad de un futuro éxito o fracaso, respectivamente.
- Si c=0 los sucesos son independientes y no se alteran las condiciones iniciales.
- Si c<0 el éxito disminuye la probabilidad de un nuevo éxito y el fracaso disminuye la probabilidad de un nuevo fracaso.
- Si c=-1: Distribución hipergeométrica.
- Si c=0: Distribución binomial.
- Si c=1: Distribución hipergeométrica negativa.
- Si c=a=N-a: Distribución uniforme discreta.
- Se puede elegir elegir el número de bolas negras 'N' y bolas rojas 'R' iniciales.
- Se pueden modificar los parámetros 'a' y 'b' de bolas de cada color que se añaden en cada iteración.
- Se puede fijar el número de iteraciones 'k'.
- Se muestran los valores y la gráfica de las sucesivas iteraciones.
- Se muestran el número de bolas negras y rojas finales y su proporción.
 |
| Descargar .XLS |
viernes, 17 de junio de 2022
Selectividad Ciencias Sociales-Curso 2021-2022
miércoles, 15 de junio de 2022
Selectividad Ciencias-Curso 2021-2022
viernes, 27 de mayo de 2022
En el espíritu de Wasan (II)
Veamos otro ejemplo sencillo que también utiliza el teorema de Pitágoras.
Una circunferencia es tangente interior a una circunferencia mayor y a su diámetro. Construir la circunferencia tangente a ambas y a ese diámetro y expresar su radio en función de la circunferencia mayor.
Sea R el radio de la circunferencia mediana de centro E y r el radio del la circunferencia buscada. En el triángulo ADE, aplicando el teorema de Pitágoras, se tiene:
$$(R+r)^2=AD^2+(R-r)^2 \rightarrow 4Rr=AD^2$$
De forma análoga, en el triángulo ABC se tiene:
$$(2R-r)^2=BC^2+r^2 \rightarrow 4R^2-4Rr=BC^2$$
Como AD=BC se tiene que:
$$4R^2-4Rr=4Rr \rightarrow 4R^2=8Rr \rightarrow R=2r$$
Entonces el centro A, del la circunferencia buscada, se puede obtener como intersección de dos circunferencias de centros C y E y de radio 3R/2.
- Los puntos azules permiten cambiar la posición y el tamaño de la figura.
- Se puede ver la construcción 'paso a paso'.
lunes, 18 de abril de 2022
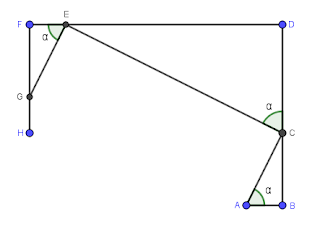
En el espíritu de Wasan (I)
Hay una palabra, wasan, que utilizan los japoneses para referirse a sus matemáticas frente a yosan o matemáticas occidentales. Aunque el wasan se debe a varios matemáticos japoneses, los iniciadores son Kambei Mori (principio siglo 17) y Yoshida Mitsuyoshi (1598-1672). Veamos un ejemplo sencillo que utiliza el teorema de Pitágoras.
Los centros A y B de dos círcunferencias iguales están en la circunferencia de la otra. Construir una circunferencia tangente a la recta AB, a la circunferencia de centro A interiormente y a la circunferencia de centro B exteriormente.
Llamamos AB=a, AF=x y GF=r (el radio de la circunferencia buscada). En el triángulo BFG, aplicando el teorema de Pitágoras, se tiene:
$$(a+r)^2=r^2+(a+x)^2$$
y , de forma análoga, en el triángulo AFG se cumple:
$$ (a-r)^2=r^2+x^2$$
Simplificando ambas ecuaciones y restando se obtiene:
$$4ar=a^2+2ax \rightarrow x+ a/2=2r$$
Significa que el lado EF del cuadrado ACDE, siendo C el punto medio del segmento AB, es un diámetro de la circunferencia buscada. Por tanto es fácil su construcción.
- Los puntos A y B permiten cambiar la posición y el tamaño de la figura.
- Se puede ver la construcción 'paso a paso'.
lunes, 28 de febrero de 2022
Método de Lill
El ingeniero y oficial del ejército austríaco Eduard Lill (1830-1900) ideó en matemáticas un procedimiento gráfico para determinar las raíces reales de un polinomio, que en esencia es una representación gráfica del algoritmo de Horner. Publicó su invento en 1867 en la revista francesa 'Nouvelles Annales de Mathématiques', y Charles Hermite proporcionó una descripción del mismo para el 'Compes rendus' del mismo año. Más tarde se conoció como el método de Lill.
El método de Lill implica expresar los coeficientes de un polinomio como magnitudes de una secuencia de segmentos en ángulos rectos entre sí. Encontrar las raíces se convierte en la realización de un problema geométrico. Vamos a explicarlo con el siguiente polinomio:
$$p(x)=1x^3+5x^2+7x+3$$
Siempre se puede hacer que el coeficiente de la potencia más alta sea la unidad, basta dividir todo el polinomio por ese valor. Se construye un primer segmento AB=1 y a continuación se construyen los segmentos perpendiculares correspondientes a los demás coeficientes del polinomio de la siguiente forma:
Hacia arriba BD=5, hacia la izquierda DF=7 y hacia abajo FH=3 porque todos los coeficientes son positivos. Cuando son negativos, se construyen en el sentido contrario a partir del extremo B. Se traza un segmento AC con el extremo en un punto cualquiera del segmento BD. Se traza el segmento CE perpendicular a AC y el segmento EG perpendicular a CE.
$$tg (\alpha)=\frac{BC}{AC}=\frac{BC}{1}=BC=-x$$
$$tg (\alpha)=\frac{BC}{AC}=\frac{BC}{1}=BC=-x \rightarrow CD=5-(-x)=5+x$$
$$tg (\alpha)=\frac{DE}{CD}=\frac{DE}{5+x}=-x \rightarrow DE=-x(5+x) \rightarrow EF=7+x(5+x)$$
$$tg (\alpha)=\frac{FG}{EF}=\frac{FG}{7+x(5+x)}=-x \rightarrow FG=-x(7+x(5+x)) \rightarrow $$
$$GH=3+x(7+x(5+x))=3+x(7+5x+x^2)=3+7x+5x^2+x^3$$
Es decir, obtenemos el polinomio pero expresado según el algoritmo de Horner.Si se divide el polinomio por x+2, se tiene:
$$\frac{1x^3+5x^2+7x+3}{x+2}=1x^2+3x+1+\frac{1}{x+2}$$
- Moviendo el punto azul se obtienen dos raíces diferentes.
- Se puede ver o no la obtención de la otra raíz doble.
- Moviendo el punto rojo se obtiene la segunda raíz doble.
- Se puede ver la construcción 'paso a paso'.
- Se puede ver la construcción 'paso a paso'.
viernes, 21 de enero de 2022
Períodos de Pisano
La operación módulo da el resto de una división entera: $$14 \mod 3 =2$$ donde 2 es el resto de dividir 14 entre 3.
Para la sucesión de Fibonacci: $$0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181...$$ la sucesión de restos, es siempre periódica: $$F_i \mod n$$
- restos modulo 2: $$0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1...$$
- restos modulo 3: $$0,1,1,2,0,2,2,1,0,1,1,2,0,2,2,1,0,1,1,2,0,2,2,1...$$
- restos modulo 4: $$0,1,1,2,3,1,0,1,1,3,2,1,0,1,1,3,2,1,0,1,1,2,3,1...$$
- restos modulo 5: $$0,1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0,1,1,2...$$
- restos modulo 6: $$0,1,1,2,3,5,2,1,3,4,1,5,0,5,5,4,3,1,4,5,3,2,5,1...$$
- restos modulo 7: $$0,1,1,2,3,5,1,6,1,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1...$$
- restos modulo 8: $$0,1,1,2,3,5,0,5,5,2,7,1,0,1,1,2,3,5,0,5,5,2,7,1...$$
- restos modulo 9: $$0,1,1,2,3,5,8,4,3,7,1,8,0,8,8,7,6,4,1,5,6,2,8,1...$$
En el caso de módulo 10, el periodo es: $$\pi(10)=\pi(2)\cdot\pi(5)=3\cdot 20=60$$ y el ciclo tiene 4 ceros y por tanto la figura es es simétrica.
- Se puede ver la construcción 'paso a paso'.