Si queremos dividir en 12 trozos o porciones iguales una tarta hexagonal o una pizza (necesariamente circular), la forma habitual es hacer cortes radiales.
En el caso de la tarta se unen con segmentos los vértices del polígono con su centro, dando origen a 6 triángulos equiláteros y posteriormente desde el centro del polígono se trazan las alturas de cada unos de los triángulos, obteniéndose así 12 triángulos rectángulos idénticos.
En el caso de la pizza se divide en 12 sectores circulares de 30 grados cada uno, que es la forma tradicional de dividir una pizza.
Matemáticos de la Universidad de Liverpool han llevado al extremo la preocupación de no pocos amantes de la pizza por compartir este popular alimento distribuyendo equitativamente las porciones.
Pero ¿y si el centro de la pizza tiene un complemento que algunas personas prefieren evitar, mientras que otros les gusta más la zona crujiente del borde?
Un estudio publicado en arXiv por Joel Haddley y Stephen Worsley explora las posibilidades y variaciones sobre una porción convencional de pizza, aunque su aplicación real sea complicada para cualquier cortador, incluso los que elaboran profesionalmente este producto.
Analizan las figuras planas monoedrales, es decir, aquellas que pueden ser teseladas mediante piezas congruentes (igual tamaño y forma).
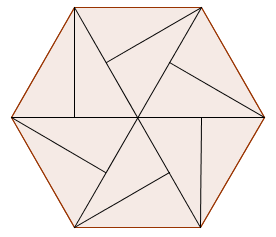
Si nos fijamos en la tarta, otra forma hubiera sido trazando cualquiera de las otras alturas de los triángulos equiláteros. Así la mitad de las porciones serían exteriores y la otra mitad interiores.
Pero ¿y si el centro de la pizza tiene un complemento que algunas personas prefieren evitar, mientras que otros les gusta más la zona crujiente del borde?
Un estudio publicado en arXiv por Joel Haddley y Stephen Worsley explora las posibilidades y variaciones sobre una porción convencional de pizza, aunque su aplicación real sea complicada para cualquier cortador, incluso los que elaboran profesionalmente este producto.
Analizan las figuras planas monoedrales, es decir, aquellas que pueden ser teseladas mediante piezas congruentes (igual tamaño y forma).
Si nos fijamos en la tarta, otra forma hubiera sido trazando cualquiera de las otras alturas de los triángulos equiláteros. Así la mitad de las porciones serían exteriores y la otra mitad interiores.
Par conseguir algo parecido con la pizza, trazaron arcos de circunferencia iguales a la sexta parte de la longitud de la circunferencia y posteriormente trazaron segmentos que dividían cada una de las 6 piezas obtenidas por la mitad, consiguiendo 12 piezas idénticas, pero la mitad exteriores y la mitad interiores.
Se puede consultar el estudio completo sobre embaldosamientos monoedales: Infinite families of monohedral disk tilings (Familias infinitas de embaldosados en discos monoedrales).



No hay comentarios:
Publicar un comentario